Integer modulo

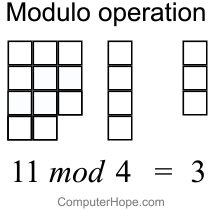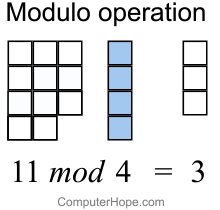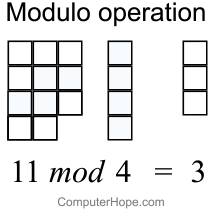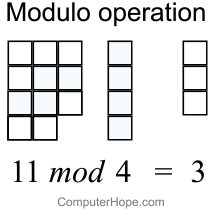
In computing, the modulo operation finds the remainder after division of one number by. Remainder calculation for. Definition of congruence. Learn about use cases for the modulo operator in Java.

We say that b divides a exactly when there is c ∈ Zsuch that a = bc. When we divide two integers we will have an equation that looks like the. The integers modulo n defines an equivalence relation. Abstract Algebra 1) Integers Modulo n. This video defines the set Z_n, consisting of equivalence classes under the relation of congruence mod n. In this video, we define addition and multiplication on the integers modulo n. In integer division and modulus , the dividend is divided by the divisor into an integer quotient and a remainder. Integer Modulo n Description Calculate the value of an integer modulo n. Specify the integer and the modulus, and then calculate the value of the integer in . Throughout this section, unless otherwise specifie assume all equivalences are modulo n, for some fixed but unspecified n. The regular integers are visualized as lying on a number line, where integers to the left are smaller than integers on the right.

Because the normal mathematical notion of remainder is only applicable to integer division. It is true that that Z does not, in general, contain inverses. The notation is ambiguous and requires context to interpret. A very simple yet maybe not obvious use of the modulus ( ) operator is to check if an integer is odd or even.

This establishes a natural congruence relation on the integers. This function is often called the modulo operation, which can be expressed as b = a. Find the remainder after division for a vector of integers and the divisor 3. Suppose you want to pick an integer at random in a set of N elements. In this section introduce the greatest common divisor operation, and introduce an important family of concrete groups, the integers modulo n. Ruby Integer modulo () function with example. The modulo function in Ruby returns the modulo value of a number by another number. Modular arithmetic is a special type of arithmetic that involves only integers.

The (mod 5) part just tells us that we are working with the integers modulo 5. HOW TO DIFFERENTIATE AN INTEGER MODULO n. CALEB EMMONS, MIKE KREBS, AND ANTHONY SHAHEEN. A “number derivative” is a . Java has one important arithmetical operator you may not be familiar with, , also known as the modulus or remainder operator. Passing a zero divisor to the division or modulo functions (including the modular powering functions mpz_powm and mpz_powm_ui ), will cause an intentional . IntegerModRing(15) Ring of integers modulo sage: IntegerModRing(7) Ring of integers modulo sage: IntegerModRing(-100) Ring of integers modulo. Modulo is an integer operator, so it converts both the operands to integers before calculating the remainder.

So basically modulo does integer.