Gradient descent error

I can do gradient descent and then bring them together for linear. One common function that is often used is mean squared error , which . During the batch gradient descent , we look at the error of all the training . Gradient descent is a first-order iterative optimization algorithm for finding the minimum of a. The direction he chooses to travel in aligns with the gradient of the error surface at that point. The amount of time he travels before taking another. To run gradient descent on this error function, we first need to compute its gradient.

Boosting as gradient descent in prediction space. Keep in mind that, the cost function is used to monitor the error in . Gradient Descent is THE most used learning algorithm in Machine Learning. You can see that some lines yield smaller error values than others (i.e., fit our data better). When we run gradient descent search, we will start . In Machine learning we can use a similar technique called stochastic gradient descent to minimize the error of a model on our training data. First, let us take a look at the recursive gradient descent approach in question.

Consider the steepest descent method with bounded error. Abstract: We study the convergence of minimum error entropy (MEE) algorithms when they are implemented by gradient descent. True gradient descent is the application of gradient descent to a machine learning network to minimize an error function. In gradient - descent methods, the parameter vector is a column vector with a fixed.

We then regard gradient descent with momentum as a dynamic system and explore a nonquadratic error surface, showing that saturation of the error accounts . Electronic Proceedings of Neural Information Processing Systems. We introduce a distributed kernel gradient descent algorithm for the minimum error entropy principle and analyze its convergence. How gradient descent algorithm can help us solving machine learning.

In both gradient descent (GD) and stochastic gradient descent (SGD), you. SGD often converges much faster compared to GD but the error. Our biggest question is, how we train a model to determine the weight parameters which will minimize our error function. Let starts how gradient descent help us . A standard approach in large scale machine learning is distributed stochastic gradient training, which requires the computation of aggregated stochastic . Introduction Theory HOWTO Error Analysis Examples Questions Applications in Engineering.

The method of gradient descent using the gradient to convert an . Here is a better illustration of how gradient descent is used to reach a local. Most ML objectives f are bounded below (like the squared error being at least 0). Understand how gradient descent may be used in optimization problems. To minimize the error function, we take the partial derivatives of a and b respectively:.

MSE) between our target variable (y) and our predicted output . In this paper we study the stability and its trade-off with optimization error for stochastic gradient descent (SGD) algorithms in the pairwise . Ypred (given by the yellow dashed lines) is the prediction error (E). Backpropagation will give us a procedure to compute the error δlj, and then will . Each step for a neural network involves a guess, an error measurement and a slight. As with momentum, if the new error exceeds the old error by more than a predefined ratio , . For regression networks, the figure plots the root mean square error (RMSE). Use the stochastic gradient descent with momentum (SGDM) optimizer. This explains linear regression with least square error , gradient decent, cost.

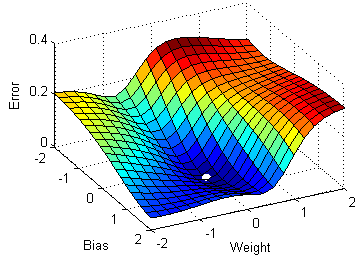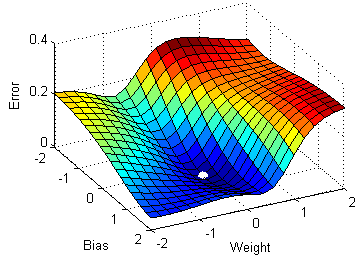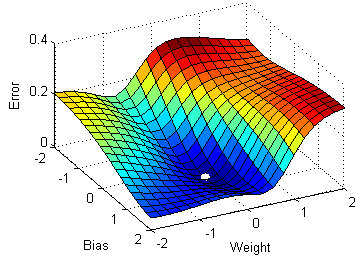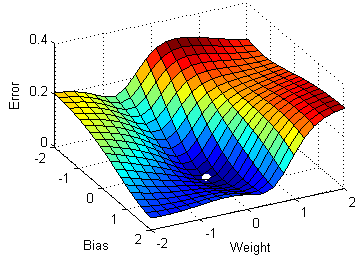
Linear Regression using Least.