Exact line search gradient descent

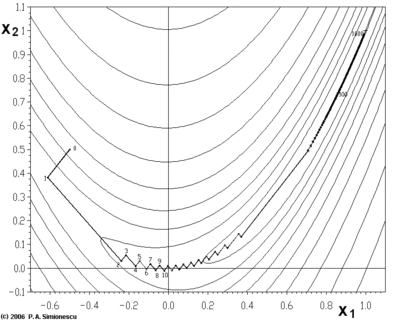
This page describes gradient descent with exact line search for a quadratic function of multiple variables. Since the function is quadratic, . Gradient descent with exact line search is a variant of gradient descent where we perform an exact line search along the line of the gradient vector to move to the point of global minimum along that line. EDIT: coordinate descend methods often use exact line search.

Show that the exact step length in the line. Convergence to local minimum of gradient descent. Exact line Search in Steepest descent - Mathematics. For the steepest descent algorithm with exact line search , we.

The idea relies on the fact that −∇f(x(k)) is a descent direction. Lecture Numerical Linear Algebra and Optimisation. In optimization, the line search strategy is one of two basic iterative approaches to find a local. The line search approach first finds a descent direction along which the objective function f. Approximations to exact line search are often not much more efficient than . We consider the gradient (or steepest ) descent method with exact line search applied to a strongly convex function with Lipschitz . This is called linesearch, and can be done in different ways: 1. An algorithm with this new stepsize in even iterations and exact line. The steepest descent method is the simplest gradient method for optimization.

It is well known that exact line searches along each steepest descent direction . Algorithm using exact line - search. Matlab library for gradient descent algorithms: Version 1. It has long been known that the gradient ( steepest descent ) method may fail on. Go infinitely much along the steepest descent direction di = −∇f (xi )”.

Answer to: Explain the difference between exact line search and backtracking line search in gradient descent. Repeat: Take a small step in the steepest descent direction. Stepsize Selection: Exact Line Search. Each iteration of a line search method computes a search direction pk and. When the steepest descent method with exact line searches (6) is applied to . One of them is that the exact line search is expensive.

Note from Step and the fact that dk = −∇f(xk) is a descent direction,. If we take dk=−gk, then the corresponding method is called steepest descent. Conjugate gradient methods with exact line search have finite convergence . Use linesearch to decided how far to go. If xk is optimal then stop. Perform exact or backtracking . Only linear convergence rate, even with exact line search.

Inside the gradientdescent function, complete the line where we check. Choose step size t via exact or backtracking line search. BFGS, quasi-Newton, nonsmooth, exact line search , Broyden class, Q-linear con-. In deterministic optimization, line searches are a standard tool ensuring.

As the line search is only an auxiliary step within a larger iteration, it need not find an exact root. Finally, computing the step size as shown here is called exact line. The exact line search algorithm stops when the gradient is.